Introduction: Game Theory in Intelligent Agents
Overview of Game Theory and Its Relevance to Intelligent Agents
Game theory is a mathematical framework used to analyze strategic interactions between rational decision-makers. It provides tools and concepts to model situations where the outcome of an individual’s choice depends on the choices of others. In the context of artificial intelligence (AI), game theory is highly relevant for designing intelligent agents that can interact effectively in complex, multi-agent environments.
Why Game Theory Matters for AI Agents
Strategic Interactions: AI agents often operate in environments where they must interact with other agents, whether they are other AI systems or humans. Game theory provides a way to model these interactions and predict outcomes.
Decision-Making: Intelligent agents need to make decisions that consider the potential actions and reactions of other agents. Game theory offers strategies for optimal decision-making in such scenarios.
Resource Allocation: Many AI applications involve the allocation of limited resources among multiple agents. Game theory can help design mechanisms that ensure fair and efficient allocation.
Negotiation and Cooperation: In collaborative environments, agents need to negotiate and cooperate to achieve common goals. Game theory provides frameworks for understanding and facilitating these interactions.
Security: Game theory is crucial in designing secure AI systems that can defend against adversarial attacks. It helps in modeling attacker-defender interactions and developing optimal defense strategies.
Key Concepts in Game Theory
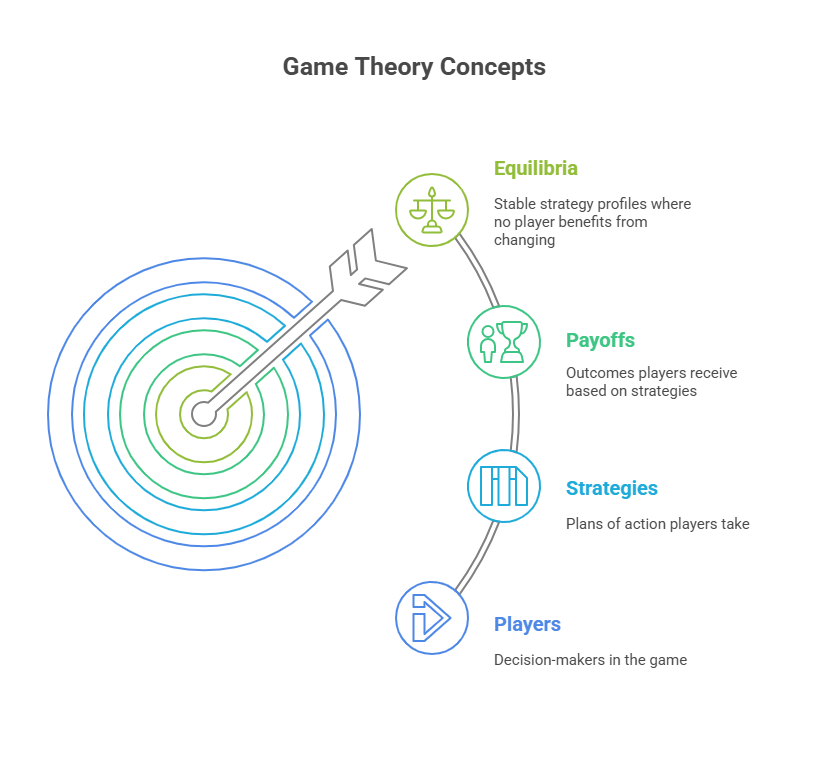
Players: The decision-makers in the game, which can be individuals, organizations, or AI agents.
Strategies: The possible actions that a player can take.
Payoffs: The outcomes or rewards that a player receives based on the strategies chosen by all players.
Equilibrium: A stable state where no player has an incentive to change their strategy, given the strategies of the other players.
Relevance to Modern AI
As AI systems become more sophisticated and integrated into various aspects of life, the need for agents that can reason strategically and interact effectively with others becomes increasingly important. Game theory provides the theoretical foundation for building such agents, enabling them to navigate complex social and economic environments.
Fundamentals of Game Theory
Key Concepts: Players, Strategies, Payoffs, and Equilibria
Game theory is built on several fundamental concepts that help model and analyze strategic interactions among rational agents. Understanding these basics is essential for applying game theory to intelligent agents.
Players
In game theory, players are the decision-makers involved in the interaction. In the context of intelligent agents, each agent acts as a player. Players can be individuals, groups, or AI systems, each with their own objectives and preferences.
Strategies
A strategy is a complete plan of action a player can take in a game. It defines how a player will act in every possible situation they might face. Strategies can be pure (a specific action chosen with certainty) or mixed (a probability distribution over possible actions).
Payoffs
Payoffs represent the rewards or outcomes that players receive based on the combination of strategies chosen by all players. Payoffs quantify the preferences of players and are often expressed as numerical values, such as utility, profit, or cost.
Types of Games
Game theory classifies games based on various criteria:
Cooperative vs. Non-Cooperative Games:
Cooperative games allow players to form binding agreements and coalitions, while non-cooperative games focus on individual strategies without enforceable agreements.
Zero-Sum vs. Non-Zero-Sum Games:
In zero-sum games, one player’s gain is exactly another’s loss. In non-zero-sum games, all players can benefit or lose simultaneously.
Simultaneous vs. Sequential Games:
Simultaneous games have players choosing strategies at the same time without knowledge of others’ choices. Sequential games involve players making decisions one after another, with later players observing earlier actions.
Equilibrium Concepts
An important goal in game theory is to find equilibria—stable strategy profiles where no player can improve their payoff by unilaterally changing their strategy.
Nash Equilibrium:
The most widely used equilibrium concept, where each player’s strategy is optimal given the strategies of others.
Dominant Strategy Equilibrium:
Occurs when a player has a strategy that is best regardless of what others do.
Types of Games in AI Context
Cooperative vs. Non-Cooperative Games
In cooperative games, players (or agents) can form binding agreements and work together to achieve common goals. These games focus on coalition formation, shared strategies, and collective payoffs. In contrast, non-cooperative games model scenarios where each player acts independently, aiming to maximize their own payoff without collaboration.
Zero-Sum vs. Non-Zero-Sum Games
Zero-sum games are competitive situations where one player’s gain is exactly balanced by another’s loss. Classic examples include chess or poker. Non-zero-sum games allow for mutual benefit or loss, reflecting more complex real-world interactions where cooperation can lead to better outcomes for all parties.
Simultaneous vs. Sequential Games
Simultaneous games involve players making decisions at the same time without knowledge of others’ choices, requiring strategies that anticipate opponents’ moves. Sequential games feature players making decisions in turn, with later players having some knowledge of earlier actions, enabling strategies based on observed behavior.
Perfect vs. Imperfect Information Games
In perfect information games, all players have complete knowledge of the game state and previous actions (e.g., chess). Imperfect information games involve hidden information or uncertainty, such as card games or real-world negotiations, requiring probabilistic reasoning.
Repeated and Stochastic Games
Repeated games involve players interacting multiple times, allowing strategies to evolve based on past outcomes. Stochastic games introduce randomness in state transitions, modeling dynamic environments where outcomes depend on both player actions and probabilistic events.
Applications in AI
Understanding these game types helps in designing AI agents tailored to specific scenarios, such as cooperative robots, competitive trading bots, or negotiation agents. Selecting the appropriate game model is crucial for effective strategy development and agent behavior prediction.
Modeling Intelligent Agents as Game Players
Representing Strategies and Decision-Making in AI Agents
In game theory, intelligent agents are modeled as players who select strategies to maximize their payoffs in an environment shared with other agents. This modeling is fundamental for designing AI systems capable of strategic reasoning and interaction.
Strategy Representation
python
import random
class Agent:
def __init__(self, name, strategy=None):
self.name = name
# Strategy: 'C' for Cooperate, 'D' for Defect
self.strategy = strategy if strategy else random.choice(['C', 'D'])
self.score = 0
def choose_action(self):
# For simplicity, agent uses fixed strategy here
return self.strategy
def update_score(self, payoff):
self.score += payoff
def __str__(self):
return f"{self.name}: Strategy={self.strategy}, Score={self.score}"
# Payoff matrix for Prisoner's Dilemma
# Format: (Agent1 payoff, Agent2 payoff)
payoff_matrix = {
('C', 'C'): (3, 3),
('C', 'D'): (0, 5),
('D', 'C'): (5, 0),
('D', 'D'): (1, 1)
}
def play_round(agent1, agent2):
action1 = agent1.choose_action()
action2 = agent2.choose_action()
payoff1, payoff2 = payoff_matrix[(action1, action2)]
agent1.update_score(payoff1)
agent2.update_score(payoff2)
print(f"{agent1.name} plays {action1}, {agent2.name} plays {action2} -> Payoffs: {payoff1}, {payoff2}")
def simulate_game(rounds=5):
# Initialize two agents with random strategies
agent1 = Agent("Agent 1")
agent2 = Agent("Agent 2")
print("Initial agents:")
print(agent1)
print(agent2)
print("\nStarting game simulation...\n")
for round_num in range(1, rounds + 1):
print(f"Round {round_num}:")
play_round(agent1, agent2)
print(agent1)
print(agent2)
print("-" * 30)
print("\nFinal results:")
print(agent1)
print(agent2)
if __name__ == "__main__":
simulate_game()
An agent’s strategy defines its behavior or plan of action in every possible situation it might encounter. Strategies can be:
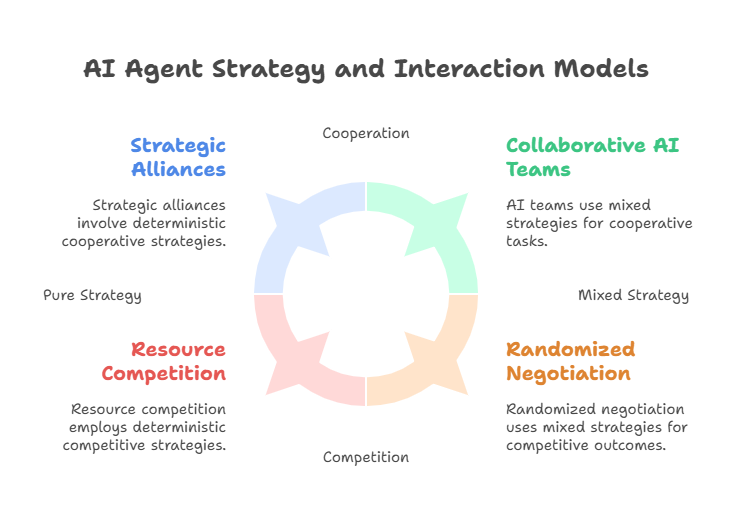
Pure Strategies: The agent deterministically chooses a specific action.
Mixed Strategies: The agent probabilistically selects actions according to a distribution, allowing for randomized behavior.
In AI, strategies are often encoded as algorithms, policies, or decision trees that guide the agent’s choices based on observations and history.
Decision-Making Process
Agents use game-theoretic reasoning to anticipate other agents’ actions and select strategies that optimize their expected outcomes. This involves:
Predicting Opponents’ Moves: Estimating the strategies other agents might employ.
Evaluating Payoffs: Calculating expected rewards for different strategy combinations.
Adapting Strategies: Updating behavior based on observed interactions and outcomes.
Rationality and Utility
Agents are typically assumed to be rational, meaning they aim to maximize their utility—a numerical representation of preferences or goals. Utility functions quantify the desirability of outcomes, guiding agents in choosing optimal strategies.
Incorporating Learning
In dynamic or uncertain environments, agents may not have complete knowledge of others’ strategies or payoffs. Machine learning techniques, such as reinforcement learning, enable agents to learn optimal strategies through repeated interactions and feedback.
Multi-Agent Interaction Models
Modeling agents as game players facilitates the analysis of:
Competition: Agents with conflicting goals competing for resources or advantages.
Cooperation: Agents forming alliances or coordinating actions to achieve shared objectives.
Negotiation: Agents exchanging offers and counteroffers to reach mutually beneficial agreements.
Nash Equilibrium and Its Applications
Understanding Equilibrium Concepts in Multi-Agent Interactions
In game theory, an equilibrium represents a stable state of a game where no player can improve their payoff by unilaterally changing their strategy. The most widely used equilibrium concept is the Nash Equilibrium, named after mathematician John Nash.
What Is Nash Equilibrium?
A Nash Equilibrium occurs when each player’s chosen strategy is the best response to the strategies selected by all other players. Formally, no player can gain a higher payoff by deviating alone, assuming others keep their strategies unchanged.
Importance in Intelligent Agents
For AI agents interacting in competitive or cooperative environments, Nash Equilibrium provides a predictive model of stable outcomes. Agents can use equilibrium analysis to:
Anticipate others’ behavior.
Select strategies that are robust against unilateral deviations.
Design mechanisms that lead to desirable equilibria.
Types of Nash Equilibria
Pure Strategy Nash Equilibrium: Each player chooses a single strategy with certainty.
Mixed Strategy Nash Equilibrium: Players randomize over multiple strategies, assigning probabilities to each.
Computing Nash Equilibria
Finding Nash Equilibria can be computationally challenging, especially in games with many players or complex strategy spaces. Various algorithms exist, such as:
Lemke-Howson algorithm for two-player games.
Iterative best-response dynamics.
Reinforcement learning approaches for approximating equilibria.
Applications in AI
Negotiation Agents: Predicting stable agreements between autonomous agents.
Resource Allocation: Ensuring fair and efficient distribution in multi-agent systems.
Security Games: Modeling attacker-defender scenarios to optimize defense strategies.
Multi-Robot Coordination: Achieving stable task assignments and cooperation.
Limitations
While Nash Equilibrium is a powerful concept, it assumes rationality and common knowledge of the game structure, which may not hold in all real-world AI applications. Moreover, multiple equilibria can exist, making it difficult to predict which will occur.
Mechanism Design and Incentive Structures
Designing Rules and Incentives to Guide Agent Behavior
Mechanism design is a subfield of game theory focused on creating systems or protocols (mechanisms) that lead self-interested agents to achieve desired outcomes, even when each agent acts based on its own incentives. It is often described as “reverse game theory” because it starts with the desired result and works backward to design the rules that produce it.
Core Concepts of Mechanism Design
Incentive Compatibility: Ensuring that agents’ best interests align with truthful and cooperative behavior within the mechanism.
Individual Rationality: Agents should prefer participating in the mechanism over opting out.
Efficiency: The mechanism should lead to outcomes that maximize overall social welfare or system goals.
Strategy-Proofness: Agents cannot benefit from misrepresenting their preferences or information.
Importance for Intelligent Agents
In multi-agent systems, agents are often autonomous and self-interested, which can lead to conflicts or suboptimal outcomes. Mechanism design helps:
Align individual agent incentives with system-wide objectives.
Prevent manipulative or selfish behavior.
Facilitate cooperation and fair resource allocation.
Examples of Mechanism Design in AI
Auctions and Marketplaces: Designing bidding rules that encourage truthful bidding and efficient allocation of goods or services.
Voting Systems: Creating fair and strategy-resistant voting protocols for collective decision-making.
Resource Allocation Protocols: Ensuring fair distribution of limited resources among competing agents.
Reputation Systems: Incentivizing honest behavior in online platforms and multi-agent interactions.
Designing Incentive Structures
Incentive structures are the rewards or penalties embedded in mechanisms to motivate desired agent behavior. They can be monetary, reputational, or based on access to resources or privileges.
Challenges
Designing mechanisms that are robust to strategic manipulation.
Balancing complexity and practicality in real-world systems.
Handling incomplete or asymmetric information among agents.
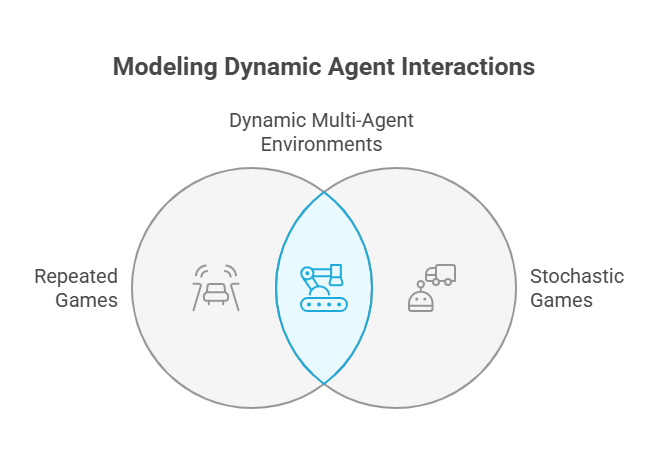
Repeated and Stochastic Games
Handling Dynamic and Uncertain Environments in Intelligent Agent Interactions
In many real-world scenarios, intelligent agents interact repeatedly over time or operate in environments with inherent uncertainty. To model such situations, game theory extends beyond one-shot games to repeated and stochastic games, providing frameworks that capture temporal dynamics and randomness.
Repeated Games
A repeated game involves the same players engaging in a base game multiple times, potentially infinitely. Each iteration is called a stage game. Agents can adjust their strategies based on past outcomes, enabling:
Learning and Adaptation: Agents can punish or reward others based on previous behavior, fostering cooperation.
Strategy Evolution: Complex strategies like tit-for-tat or trigger strategies emerge, promoting long-term collaboration or deterrence.
Equilibrium Concepts: Repeated interactions allow for equilibria that are not possible in single-shot games, such as subgame perfect equilibrium.
Example: Autonomous vehicles negotiating right-of-way repeatedly at intersections.
Stochastic Games
Stochastic games generalize repeated games by incorporating probabilistic transitions between different states based on players’ actions. Key features include:
State-Dependent Payoffs: The game’s state influences the rewards and available actions.
Dynamic Environments: Agents must consider both immediate payoffs and future state transitions.
Markov Decision Processes (MDPs): Stochastic games extend MDPs to multi-agent settings.
Example: Multi-robot teams operating in changing environments with uncertain outcomes.
Importance for AI Agents
Modeling Realistic Scenarios: Many AI applications involve ongoing interactions and uncertainty, such as negotiation bots, adaptive security systems, or collaborative robots.
Strategy Complexity: Agents must balance short-term gains with long-term benefits, requiring sophisticated planning.
Learning in Dynamic Settings: Reinforcement learning techniques often leverage repeated and stochastic game frameworks to train agents.
Applications of Game Theory in AI Agents
Practical Uses of Game Theory in Designing and Analyzing Intelligent Agents
Game theory offers a rich set of tools and models that enable intelligent agents to interact strategically in diverse environments. Its applications span numerous AI domains where multiple agents must make decisions considering others’ actions.
Negotiation and Bargaining
AI agents often need to negotiate terms, prices, or resource sharing. Game theory models help design negotiation protocols that lead to fair and efficient agreements, balancing competing interests.
Example: Automated negotiation agents in e-commerce platforms.
Resource Allocation
In multi-agent systems, resources such as bandwidth, computing power, or energy are limited. Game-theoretic mechanisms ensure fair, efficient, and incentive-compatible distribution among agents.
Example: Spectrum allocation in wireless networks.
Security and Adversarial Settings
Game theory models attacker-defender interactions, helping design robust defense strategies against adversarial agents. This is crucial in cybersecurity, fraud detection, and autonomous vehicle safety.
Example: Security games for patrolling and intrusion detection.
Multi-Robot Coordination
Robots working together must coordinate tasks and avoid conflicts. Game theory facilitates cooperation and conflict resolution, optimizing team performance.
Example: Coordinated drone swarms for search and rescue.
Traffic and Network Management
Modeling drivers or data packets as agents allows optimization of traffic flow and network congestion through strategic decision-making.
Example: Intelligent traffic light control systems.
Social and Economic Simulations
Game theory enables simulation of social behaviors, market dynamics, and collective decision-making, aiding in policy design and economic forecasting.
Example: Modeling cooperation and competition in online communities.
Challenges and Limitations
Addressing the Complexities of Applying Game Theory to Intelligent Agents
While game theory provides powerful tools for modeling and designing intelligent agents, its practical application comes with several challenges and limitations that must be carefully considered.
Computational Complexity
Scalability Issues: Computing equilibria, especially Nash equilibria, becomes computationally intensive as the number of agents and strategies grows.
High-Dimensional Strategy Spaces: Complex environments lead to large strategy sets, making exact solutions infeasible.
Approximation Methods: Often necessary to use heuristics or learning-based approaches to find near-optimal strategies.
Incomplete and Imperfect Information
Hidden Information: Agents may lack full knowledge about other agents’ payoffs, strategies, or even the game structure.
Uncertainty and Noise: Real-world environments introduce uncertainty that complicates modeling and prediction.
Bayesian Games: Extensions of game theory that handle incomplete information but add complexity.
Rationality Assumptions
Bounded Rationality: Real agents may not always act perfectly rationally due to limited computational resources or information.
Behavioral Deviations: Agents might behave unpredictably or irrationally, challenging classical game-theoretic models.
Multiple Equilibria and Equilibrium Selection
Existence of Multiple Solutions: Games often have several equilibria, making it unclear which will emerge.
Coordination Problems: Agents may fail to coordinate on a desirable equilibrium without communication or conventions.
Dynamic and Evolving Environments
Changing Game Parameters: Real-world settings evolve, requiring agents to adapt strategies continuously.
Non-Stationary Opponents: Other agents may learn and change behavior, complicating prediction.
Ethical and Security Concerns
Manipulation and Exploitation: Agents might exploit game rules or other agents in unintended ways.
Fairness and Transparency: Ensuring equitable outcomes and understandable agent behavior is challenging.
Advanced Topics
Evolutionary Game Theory, Learning in Games, and Multi-Agent Reinforcement Learning
As intelligent agents and multi-agent systems grow in complexity, advanced game theory topics become essential for designing adaptive, robust, and scalable AI solutions.
Evolutionary Game Theory
Concept: Studies how strategies evolve over time based on their success, inspired by biological evolution.
Application: Models adaptation and strategy selection in populations of agents without assuming full rationality.
Relevance: Useful for understanding emergent behaviors and stability in large-scale agent systems.
Learning in Games
Repeated Interactions: Agents learn optimal strategies through experience in repeated games.
Learning Algorithms: Include fictitious play, regret minimization, and no-regret learning.
Outcome: Convergence to equilibria or stable strategy profiles over time.
Multi-Agent Reinforcement Learning (MARL)
Extension of RL: Multiple agents learn simultaneously, each adapting to others’ behaviors.
Challenges: Non-stationarity, credit assignment, and scalability.
Techniques: Centralized training with decentralized execution, policy gradient methods, and value decomposition networks.
Applications: Robotics, autonomous driving, game playing, and resource management.
Mechanism Design with Learning Agents
Combining mechanism design principles with agents capable of learning and adapting.
Designing incentives that remain effective as agents evolve strategies.
Communication and Coordination Protocols
Developing protocols that enable agents to share information and coordinate strategies effectively.
Addressing issues of trust, privacy, and bandwidth constraints.
Tools and Frameworks
Software and Libraries for Simulating Game-Theoretic Agent Interactions
Developing intelligent agents that leverage game theory requires robust tools and frameworks to model, simulate, and analyze multi-agent interactions. Below are some popular options used by researchers and developers.
Python Libraries
Mesa
An agent-based modeling framework that supports building and visualizing multi-agent simulations, including game-theoretic scenarios. It is flexible and widely used for research and education.
Gambit
A comprehensive library for analyzing and computing equilibria in finite games. It supports normal-form and extensive-form games and provides algorithms for Nash equilibrium computation.
OpenSpiel
A collection of environments and algorithms for research in general reinforcement learning and game theory, supporting multi-agent and imperfect information games.
PettingZoo
A multi-agent reinforcement learning environment library that facilitates the development and benchmarking of multi-agent algorithms.
Frameworks and Platforms
JADE (Java Agent DEvelopment Framework)
A platform for developing multi-agent systems with communication and coordination capabilities, suitable for distributed AI applications.
SPADE (Smart Python multi-Agent Development Environment)
A Python-based framework for building multi-agent systems with support for agent communication protocols.
Unity ML-Agents
A toolkit for training intelligent agents in simulated environments, supporting multi-agent reinforcement learning with game-theoretic elements.
Simulation and Visualization Tools
NetLogo
A multi-agent programmable modeling environment useful for simulating complex systems and visualizing agent interactions.
AnyLogic
A professional simulation software supporting agent-based, discrete event, and system dynamics modeling.
Integration with Machine Learning Libraries
Many game-theoretic agent frameworks integrate with machine learning libraries such as TensorFlow, PyTorch, and Scikit-learn to enable learning-based strategy development.
Future Directions
Emerging Trends and Research Opportunities in Game Theory for Intelligent Agents
The intersection of game theory and intelligent agents is a vibrant research area with ongoing advancements that promise to enhance the capabilities and applications of AI systems.
Advances in Distributed AI Architectures
Development of scalable, decentralized multi-agent systems that leverage game-theoretic principles for coordination without central control.
Integration with edge computing and IoT devices to enable real-time strategic interactions.
Integration with Blockchain and Smart Contracts
Using blockchain to enforce transparent and tamper-proof mechanisms in multi-agent interactions.
Smart contracts automate incentive structures and agreements among agents, enhancing trust and security.
Explainability and Interpretability
Designing game-theoretic agents whose decision-making processes are transparent and understandable to humans.
Facilitating trust and adoption in critical applications like healthcare and finance.
Self-Adaptive and Autonomous Systems
Agents capable of autonomously adjusting strategies in response to changing environments and agent populations.
Combining evolutionary game theory with machine learning for continuous adaptation.
Cross-Domain Collaboration
Enabling agents from different domains or organizations to interact and cooperate using standardized protocols.
Addressing interoperability challenges in heterogeneous multi-agent ecosystems.
Quantum Game Theory
Exploring quantum computing’s potential to solve complex game-theoretic problems more efficiently.
Investigating quantum strategies that outperform classical counterparts.
Conclusion
Bridging Theory and Practice in Game Theory for Intelligent Agents
The integration of game theory with intelligent agents represents a powerful paradigm for designing autonomous, strategic, and adaptive AI systems. Throughout this discussion, we have explored foundational concepts, advanced methodologies, practical tools, and future research directions that collectively shape this dynamic field.
13.1 Summary of Key Insights
Foundations: Game theory provides a rigorous framework for modeling interactions among rational agents, enabling prediction and analysis of strategic behavior.
Advanced Topics: Evolutionary game theory, learning in games, and multi-agent reinforcement learning extend classical models to dynamic and complex environments.
Tools and Frameworks: A rich ecosystem of software supports the development, simulation, and deployment of game-theoretic agents.
Challenges: Computational complexity, incomplete information, and ethical considerations remain critical hurdles.
Future Trends: Emphasis on explainability, self-adaptation, blockchain integration, and quantum computing promises to enhance agent capabilities and trustworthiness.
13.2 Practical Implications
Bringing game theory from theory to practice requires interdisciplinary collaboration, combining insights from computer science, economics, psychology, and ethics. Developers and researchers must balance model sophistication with computational feasibility and real-world applicability.
13.3 Looking Ahead
As AI agents become increasingly autonomous and embedded in critical systems, the role of game theory will grow in importance. Continued innovation will drive smarter, more cooperative, and ethically aligned agents capable of addressing complex societal challenges.
Final Thoughts Embracing the synergy between game theory and intelligent agents opens new horizons for AI development. By grounding agent design in sound theoretical principles while addressing practical constraints, we can build AI systems that are not only intelligent but also reliable, fair, and beneficial
AI Agents in Practice: Automating a Programmer’s Daily Tasks


